Definition of torque

In physics, torque refers to the tendency of a force to cause an object to rotate around an axis or pivot. The unit of torque is Newton meter. The Greek letter for torque is tau. The concept of torque originated from Archimedes' study of levers. The rotational torque is also known as torque or torque. Torque can cause an object to change its rotational motion. Pushing or dragging involves force, while twisting involves torque. The torque is equal to the cross product of the radial vector and the applied force.

The tenancy of a force to make an object rotate

Moment of force is a physical quantity that produces a rotational effect on an object. It can be divided into moments of force on the axis and moments of force on the point. Namely: M=LxF. Where L is the distance vector from the axis of rotation to the point of force, and F is the vector force; Torque is also a vector.

The moment of force on an axis is a physical quantity that produces a rotational effect of force on an object about a certain axis. Its magnitude is equal to the product of the component of force on a plane perpendicular to that axis and the distance from the line of action of this component to the axis. For example, when opening the door, the component force F П of the external force F parallel to the door axis cannot produce a rotational effect on the door (Figure 1), because this force has been balanced by the constraint force of the fixed axis (see constraint). The force that can rotate the door is the component force F ⊥ of F in the plane perpendicular to the door axis, with the value F ⊥=Fcos α. Make a plane П perpendicular to the axis from point A of action F, intersecting the axis at point O. According to the experiment, the rotational effect of force F on an object is proportional to the vertical distance l from O to F ⊥. L is called the force arm of F ⊥ on the axis, which is equal to rsin β, where r=OA; β is the angle between F ⊥ and OA. Therefore, the rotational effect of force F on an object is determined by the product of Fcos α and rsin β, and this physical quantity is called the moment of force F on the axis, which is an algebraic quantity. When α=0 ° and β=90 °, the moment of force F on the axis is large. Therefore, to improve rotational efficiency, the force F should be in the vertical plane of the axis and perpendicular to the connecting line OA. If force F is in the vertical plane of the axis (Figure 2), the moment of force on the axis is rVsin β. This quantity can also be expressed as twice the area of △ ORB, where AB=F.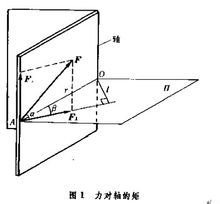

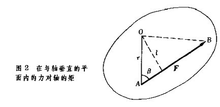
The moment of force on a point is a physical quantity that produces a rotational effect on an object around a certain point, equal to the vector product of the position vector of the point of force and the force vector. For example, an object fixed to point O with a ball joint is subjected to the instantaneous force F, where the point of action of F is A, r represents the position vector of A, and the angle between r and F is α (Figure 3). If an object is originally stationary, it will rotate along a plane perpendicular to r and F and pass through the instantaneous axis of point O after being subjected to force F. The magnitude of the rotational effect is represented by rVsin α. Due to the directional nature of the instantaneous axis, the moment of force F to point O is defined as a vector, denoted by M, i.e. M=r × F. The positive direction of M can be determined by the right-hand rule (Figure 4); The size of M is equal to twice the area of a triangle with sides r and F.

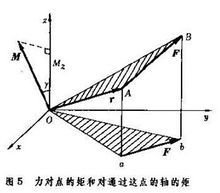
The moment M of force F on point O has three projections Mx, My, and Mz on the Cartesian axis passing through the centroid O. It can be proven that Mz is the moment of F on the z-axis (Figure 5).

The 'axis' and' point 'in the above torque concept are both taken from physical objects. But when studying mechanical problems, it is not necessary to consider these physical objects, and the moment of force to a point and the moment of force to an axis can be defined for any point and line in space.

The dimension of torque is force x distance; Same dimensional as energy. But torque is usually measured in Newton's terms

-Meter, instead of using joules as a unit. The unit of torque is determined by the units of force and force arm.

fold